Artificial Neural Networks

Neural network playground

https://playground.tensorflow.org/

Basic working mechanism

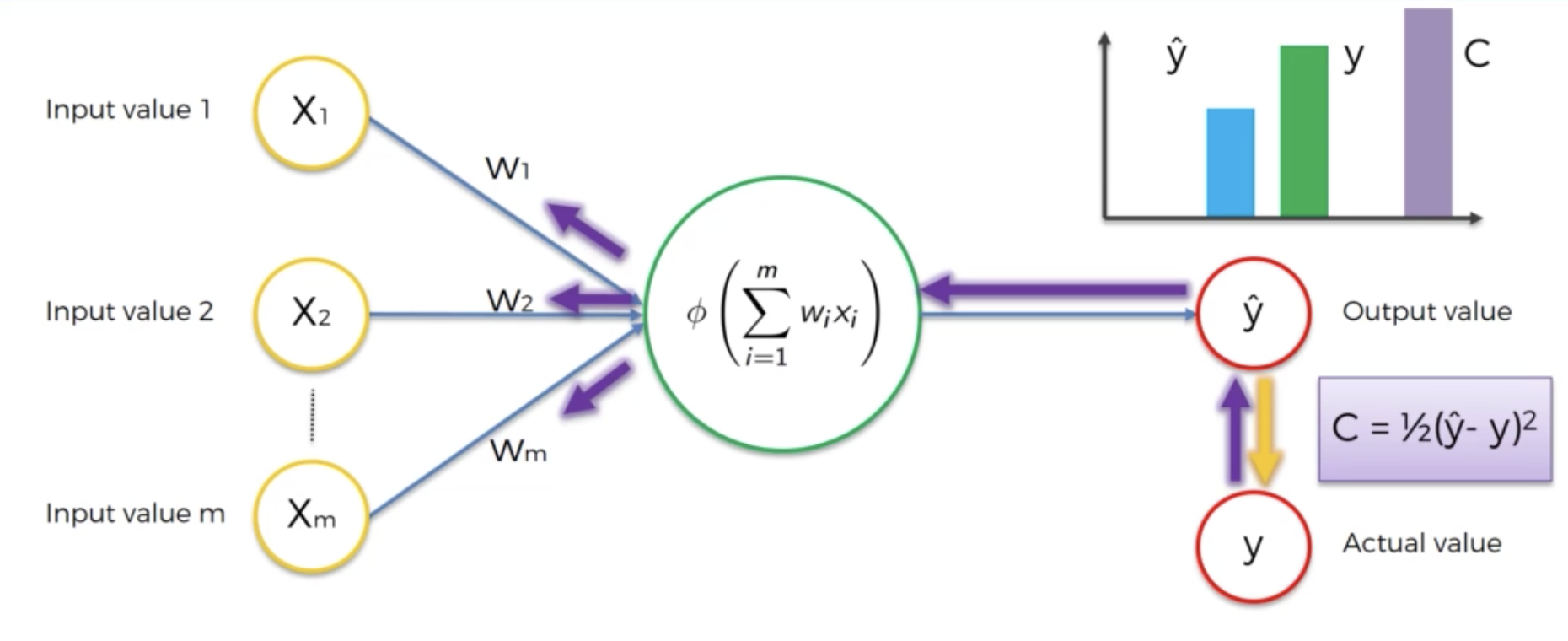
How it works

Randomly initialise the weights to small numbers close to 0 (but not 0).
Input the first observation of your dataset in the input layer, each feature in one input node.
Forward-propagation: from left to light, the neurons are activated in a way that the impact of each neuron's activation is limited by the weights. Propagate the activations until getting the predicted result y.
Compare the predicted result to the actual result. Measure the generated error.
Back-propagation: from right to left, the error is propagated. Update the weights according to how much they are responsible for the error. The learning rate decides by now much we update the weights.
Repeat Steps 1 to 5 and update the weights after each observation (Reinforcement Learning); OR: Repeat Steps 1 to 5 but update the weights only after a batch of observations (Batch Learning).
When the whole training set passed through the ANN, that makes an epoch. Redo more epochs.

Epoch vs. Batch

1 batch = a group of samples
1 epoch = touching each sample once, which contains multiple batches

Activation functions

There are multiple forms

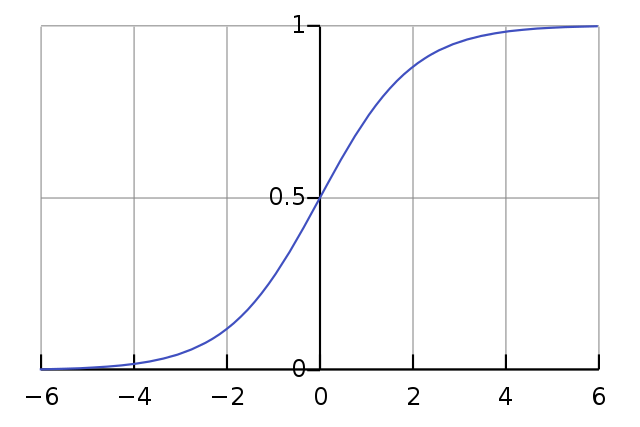
sigmoid

ϕ (z) = \frac{1}{1 + e^{z}}

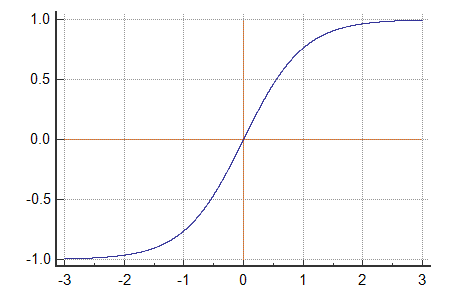
tanh = a shifted sigmoid with a mean as 0

ϕ (z) = \frac{e^{z} - e^{- z}}{e^{z} + e^{- z}}

Softmax

ϕ (z) = Softmax (z_{i}) = \frac{\exp (z_{i})}{\sum_{j} \exp (z_{j})}

Why "soft": because it generates values between 0 and 1 and sum to 1, so the max value is a probability smaller than 1, instead of "hard" max value as 1 and the rest as 0.

rectifier (ReLU) - when you must model a piecewise linear target

ϕ (z) = m a x (z, 0)

An alternative (better) version of ReLU is leaky ReLU.

Linear activation function

ϕ (z) = a z + b

Hyperbolic Tangent (tanh)

ϕ (z) = \frac{1 - e^{- 2 z}}{1 + e^{- 2 z}}

Which to choose depends on your problems:

for the output layer:
- binary classification -> sigmoid
- multiclass classification -> Softmax
- regression -> linear activation & ReLU
for hidden layers:
- use default function (usually ReLU, because it is faster)
Andrew Ng:
If you're not sure what to use for your hidden layer, I would just use the ReLu activation function that's what you see most people using these days.
- tanh is better than sigmoid
- do not use linear activation
Different forms can be combined, e.g. using rectifier in the hidden layer and then sigmoid in output layer

Why ReLU is faster than sigmoid-like activation functions?

Because minimizing loss function requires Notes/Gradient Descent, whose speed depends on the derivative of the activation function $ϕ (z)$ . Both derivatives of sigmoid and tanh functions become very small when $ϕ (z)$ , in other words, gradient descent becomes very slow. But this won't happen to ReLU, because its derivative is a constant (when $z > 0$ ).